Think more rationally with Bayes’ rule

Think more rationally with Bayes’ rule
Photo by Wim van 't Einde / Unsplash

Bayes' rule is a powerful mathematical tool that can be used to make rational decisions based on available evidence. It was developed by the English mathematician Thomas Bayes in the 18th century and is widely used in areas such as data science, artificial intelligence, and decision theory.

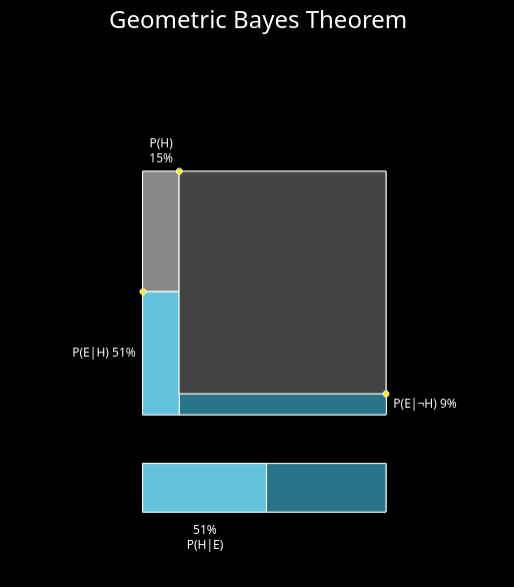
https://www.skobelevs.ie/BayesTheorem/

Bayes' rule establishes a relationship between the conditional probability of an event A, given an event B, and the marginal probabilities of A and B. Formally, it can be written as:

P(A|B) = P(B|A) * P(A) / P(B)

Where:

  • P(A|B) is the conditional probability of A, given B.
  • P(B|A) is the conditional probability of B, given A.
  • P(A) is the marginal probability of A.
  • P(B) is the marginal probability of B.


Bayes' rule can be used in different contexts to answer different questions. For example, it can be used to:

 - Diagnose diseases: what is the probability of a person having a certain disease, given that they have certain symptoms?

 - Detect fraud: what is the probability of a transaction being fraudulent, given that it occurred at an unusual time and in a different geographic region from the cardholder?

 - Classify documents: what is the probability of a particular document belonging to a particular category, given that it contains certain keywords?

Bayes' rule can also be used to update probabilities as new evidence is found. For example, if a diagnostic test has a certain rate of false positives and false negatives, Bayes' rule can be used to adjust the probability of a person having a certain disease, given the test result.

However, Bayes' rule has some limitations. It requires that conditional and marginal probabilities be known with precision, which can be difficult in some situations. Additionally, it assumes that evidence is independent, which may not be the case in some real-world situations.

In summary, Bayes' rule is a powerful tool for making rational decisions based on available evidence. It is widely used in areas such as data science, artificial intelligence, and decision theory. However, it has some limitations and should be used with care and a clear understanding of its assumptions and limitations.

If you want to learn more about Bayes' rule and its applications, check out this informative video: